
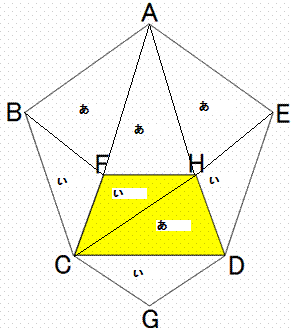
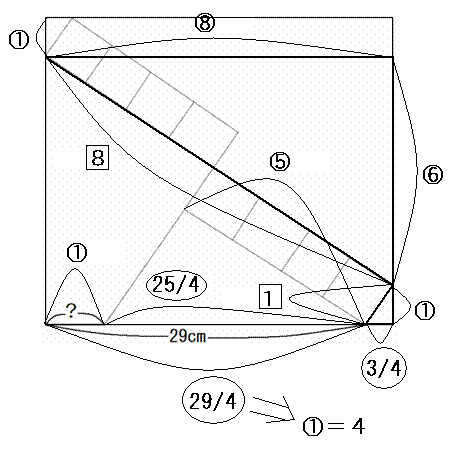
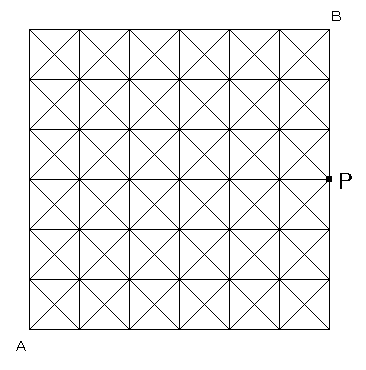
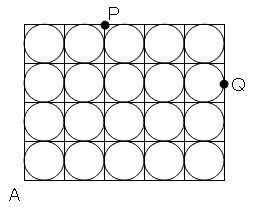
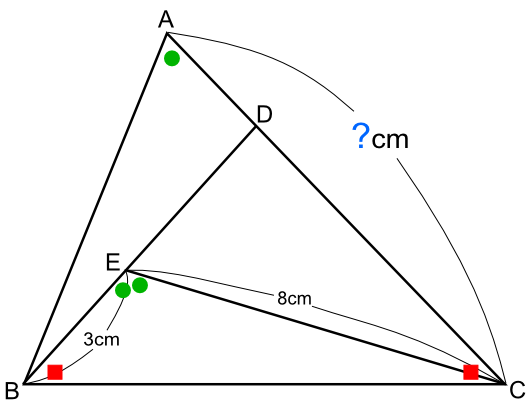
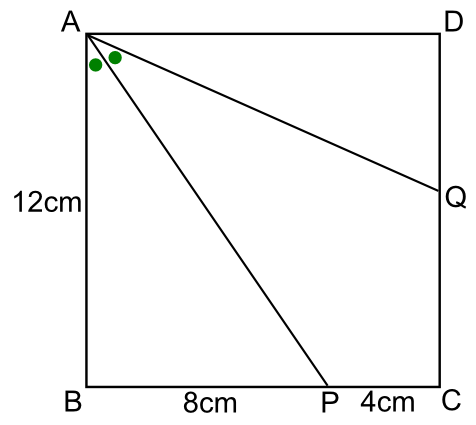
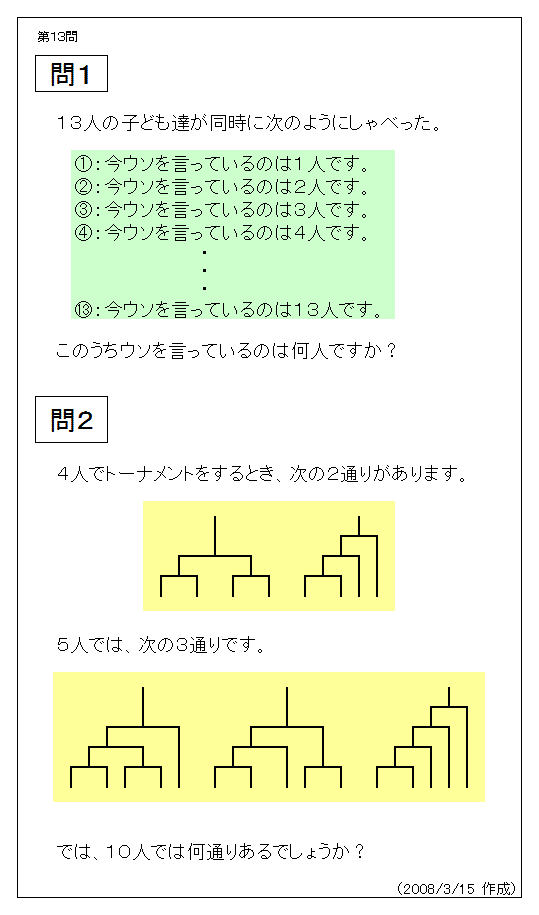
仏乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗仏
乥n恖偺偲偒偺帋崌宍幃偺悢傪a[n]偲偡傞偲丄丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乥
乥乮傾乯n=2m+1 偺偲偒丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乥
乥丂a[n]=a[1]*a[n-1]+a[2]*a[n-2]+乧乧+a[m]*a[m+1]丂丂丂丂丂丂丂丂丂丂丂 乥
乥乮僀乯n=2m 偺偲偒丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乥
乥丂a[n]=a[1]*a[n-1]+a[2]*a[n-2]+乧乧+a[m-1]*a[m+1]+{(a[m]+a[m]^2)/2}丂 乥
仏乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗仏
妋偐偵寢峔擄栤偱偡丅
| 弴埵丂(1) | 偍柤慜丂(2) | 夞摎擔帪 | ||
|---|---|---|---|---|
| 侾 | 僟儞僨傿奀栰偝傫 | 2008擭3寧16擔 (擔) 屵慜11帪51暘49昩 | ||
| 俀 | MP5K偝傫 | 2008擭3寧16擔 (擔) 屵慜12帪18暘46昩 | ||
| 俁 | 僗儌乕僋儅儞偝傫 | 2008擭3寧18擔 (壩) 屵屻2帪24暘30昩 | ||
| 係 | 傐偮偝傫 | 2008擭3寧18擔 (壩) 屵屻7帪47暘8昩 | ||
| 俆 | weapon偝傫 | 2008擭3寧18擔 (壩) 屵屻11帪41暘9昩 | ||
| 俇 | 冄偝傫 | 2008擭3寧20擔 (栘) 屵慜0帪36暘54昩 | ||
| 俈 | nakakun偝傫 | 2008擭3寧20擔 (栘) 屵屻7帪33暘59昩 | ||
| 俉 | p偝傫 | 2008擭3寧23擔 (擔) 屵慜10帪36暘23昩 | ||
| 俋 | N偝傫 | 2008擭3寧29擔 (搚) 屵屻8帪13暘49昩 | ||
| 侾侽 | atsuka偝傫 | 2008擭4寧3擔 (栘) 屵慜0帪38暘13昩 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 3 |
| 2 | |||
| 1 |
| 弴埵 | 偍柤慜 | 夞摎擔帪 | ||
|---|---|---|---|---|
| 侾 | 俵倰丏僟儞僨傿偝傫 | 2008擭4寧5擔 (搚) 屵慜0帪0暘26昩 | ||
| 俀 | weapon偝傫 | 2008擭4寧5擔 (搚) 屵屻2帪12暘43昩 | ||
| 俁 | NN偝傫 | 2008擭4寧5擔 (搚) 屵屻2帪44暘2昩 | ||
| 係 | nakakun偝傫 | 2008擭4寧18擔 (嬥) 屵屻6帪58暘1昩 |
| 弴埵 | 偍柤慜 | 夞摎擔帪 | ||
|---|---|---|---|---|
| 侾 | kasama偝傫 | 2008擭4寧19擔 (搚) 屵慜2帪19暘40昩 | ||
| 俀 | uchinyan偝傫 | 2008擭4寧19擔 (搚) 屵屻11帪50暘33昩 | ||
| 俁 | nakakun偝傫 | 2008擭4寧20擔 (擔) 屵慜2帪58暘34昩 | ||
| 係 | 偡偖傞妛廗夛偝傫 | 2008擭4寧20擔 (擔) 屵慜7帪40暘33昩 | ||
| 俆 | kata偝傫 | 2008擭4寧20擔 (擔) 屵屻7帪22暘28昩 | ||
| 俇 | NN偝傫 | 2008擭4寧22擔 (壩) 屵屻7帪24暘48昩 | ||
| 俈 | 傂偖傝傫偝傫 | 2008擭4寧23擔 (悈) 屵屻3帪11暘54昩 | ||
| 俉 | 悈揷X偝傫 | 2008擭4寧24擔 (栘) 屵慜9帪6暘0昩 | ||
| 俋 | 俵倰丏僟儞僨傿偝傫 | 2008擭4寧25擔 (嬥) 屵屻6帪35暘1昩 | ||
| 侾侽 | 壊鍄偝傫 | 2008擭4寧25擔 (嬥) 屵屻7帪18暘28昩 |